Le cercle des points disparus
Au cours d’un exercice de maths1 dans ma classe de seconde, les élèves affirment par un vote quasi unanime que chacune des trois phrases suivantes est vraie :
1) il y a deux fois plus de points sur le cercle que sur la droite (et même deux de plus encore)
2) il y a une infinité de points sur la droite (parce qu’elle est infinie des deux côtés)
3) il n’y a pas une infinité de points sur le cercle (parce qu’il est fermé)
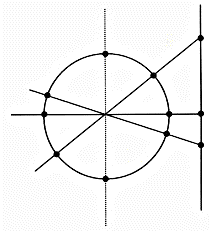
Certains remarquent que les trois phrases ne peuvent pas être simultanément vraies, et la discussion se poursuit en demi groupe.
Résumé de la discussion dans le premier groupe :
- sur le cercle, c’est comme sur un segment, il n’y a qu’un nombre fini de points, parce que c’est limité, et donc on ne peut caser qu’un certain nombre de points ;
- mais comment sont "rangés" les points sur la droite, le cercle, le segment ? Quand on voit deux points, on peut mettre un autre point entre les deux, sauf si ces deux points se touchent ; et à force d’en rajouter, il y a un moment où ils vont se toucher, et là, c’est fini !
La discussion est assez vive, et n’amène pas de conclusion définitive (certains élèves ayant en outre déclaré que ce n’était pas vraiment la peine de "se prendre la tête" trop longtemps là-dessus…).
Résumé de l’absence de discussion dans le deuxième groupe :
Un élève, d’un seul coup d’un seul :
- un segment, c’est comme un intervalle de nombres, par exemple, entre -1 et 1.
- on voit bien qu’il y ait une infinité de nombres entre -1 et 1, parce que, par exemple, entre 0,9 et 1, il y a 0,99 et 0,999 et 0,9999 etc.
Tout le groupe est immédiatement convaincu qu’il y a une infinité de points sur le segment et sur le cercle !
Moralité : quelques siècles après Descartes, les nombres, c’est quand même plus concret que la géométrie.
Karin van Effenterre
1. Mathématiques Seconde, Sigmath, Hatier, p. 213.
Pénombre, Mars 2000
- | Accessibilité |
- Informations légales |
- Plan |
- Contact
