Pénombre, la vie publique du nombre

--

Le test statistique et le jugement de culpabilité

L’analogie entre ces deux démarches est si forte qu’elle est souvent citée dans des cours de statistique, la seconde étant évoquée pour illustrer la première. Nulle revue n’était donc aussi indiquée que Pénombre pour exposer cette similitude. Rappelons d’abord le but et la nature du test satistique.
 

L’impossible certitude

Nous choisirons l’exemple suivant. Dans une race de souris, la fréquence des cancers spontanés est bien connue, mettons… 40%. C’est dire que, pour chaque souris, le résultat dépend d’une loterie avec 40% de billets « cancer » ; sur un échantillon de cent souris le nombre de cancéreuses varie, d’une fois à l’autre, autour de quarante selon les « fluctuations d’échantillonnage », c’est-à-dire les caprices du hasard. De vrais caprices, imprévisibles et parfois grandioses : zéro à cent cancers sont des résultats certes improbables, mais pas impossibles.

Voici maintenant qu’un biologiste veut savoir si sa dernière invention, la drogue D, modifie cette fréquence (dans un sens ou dans l’autre)¹. À cet effet, il entreprend une expérience, administrant la drogue à, par exemple, cent souris. Il observe un certain pourcentage de cancers. Comment va-t-il conclure ?

La démarche adoptée pendant des siècles était la suivante : la drogue sera dite active ou inactive selon que l’écart entre la fréquence observée et 40% sera grand ou petit. Mais que veut dire « grand » ? Que veut dire « petit » ?

Si la drogue est inactive, le pourcentage observé fluctue autour de 40%, mais les caprices du hasard pourront conduire beaucoup plus loin de 40%. Inversement, si la drogue est active et fait passer la probabilité de cancer à, par exemple, 30%, la fréquence observée sur cent souris va fluctuer autour de 30%, mais les caprices du hasard pourront conduire tout près de 40%. Ainsi drogue active ou inactive ne veut pas dire forcément écart grand ou petit. La conclusion de cette réflexion est très claire : il est impossible de se prononcer avec certitude : la « vérité » est hors de portée. C’est dans cette situation d’impossible certitude qu’une solution est apportée par le test statistique.
 

Le test statistique

Le hasard a ses caprices, mais aussi ses lois : les lois de probabilité. Sur nos cent souris, en l’absence de drogue, la fréquence des cancers pourra certes s’écarter beaucoup de 40%, mais un grand écart est improbable, d’autant plus improbable qu’il est plus grand. Le calcul des probabilités indique que, pour un échantillon de cent souris, l’écart a, par exemple :

- 5 chances sur 100 de dépasser 10% (pourcentage observé compris entre 30% et 50%).

- 1 chance sur 1’000 de dépasser 17% (pourcentage observé compris entre 23% et 57%).

En d’autres termes, on peut parier que le pourcentage de cancers tombera dans l’intervalle 30% - 50%, ou 23% - 57% avec 5 chances sur 100 ou 1 chance sur 1’000 respectivement de se tromper.

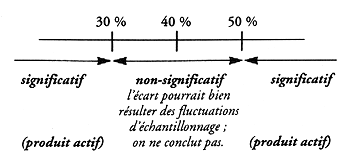
Administrons maintenant la drogue D à 100 souris. Supposons la drogue inactive, les écarts à 40% seront régis par les règles énoncées ci-dessus. Adoptons alors la politique suivante : si le pourcentage tombe en dehors de l’intervalle 30% - 50% l’écart à 40% sera dit significatif ; nous conclurons que la drogue est active. Si au contraire le pourcentage tombe à l’intérieur de cet intervalle, on admettra que l’écart à 40% pourrait bien résulter des seules fluctuations d’échantillonnage, et il sera dit non significatif ; on ne conclura pas.

Cette politique conduira certes à des erreurs : avec un produit inactif, le pourcentage sortira quand même, de temps à autre, de l’intervalle, et on déclarera le produit actif ; mais ce risque d’erreur est connu, c’est 5%. Comme il est chagrinant de se tromper, on peut adopter une politique plus sévère, et préférer un risque d’erreur de seulement 1 pour 1000. D’après le résultat présenté ci-dessus, l’intervalle de non conclusion deviendra 23% - 57% beaucoup plus grand que le précédent, on a beaucoup plus de chances de laisser échapper un produit actif : à vouloir diminuer un risque, on en augmente un autre. On ne peut donc diminuer à volonté le risque d’erreur, il faut s’arrêter à une valeur raisonnable. Une valeur très couramment admise est 5%. Ce « fameux » 5% intrigue les non initiés qui voient dans ce seuil un inexplicable « couperet ». En fait, ce seuil n’est choisi que comme un moyen terme acceptable et commode pour diverses raisons : d’abord ce risque d’erreur est faible, ensuite il conduit, pour le calcul, à une formule relativement simple, facile à retenir. Et puis c’est un chiffre rond, d’autant plus qu’on a longtemps exprimé l’erreur en termes de paris, et qu’admettre le risque 5% revient pratiquement à parier à 20 contre 1. Il est bien entendu toujours possible d’adopter un seuil différent, le « timide » par exemple le choisissant plus faible, quitte à laisser plus souvent échapper une différence.

L’examen du bilan et des risques suscite des remarques pour lesquelles l’analogie judiciaire est le plus souvent éclairante.
 

La dissymétrie des attitudes

On aura remarqué que si le pourcentage tombe à l’extérieur de l’intervalle, on conclut à l’activité de la drogue (avec un risque d’erreur), tandis que s’il tombe à l’intérieur, on ne dira pas pour autant que la drogue est inactive, c’est-à-dire que le taux vrai égale exactement 40%, ce qui serait une affirmation beaucoup trop précise, on dira seulement qu’on ne rejette pas cette hypothèse. C’est la situation de « non conclusion ». Une comparaison fera comprendre le pourquoi de la dissymétrie entre les deux attitudes, (conclusion avec risque d’erreur consenti dans le premier cas, non conclusion dans le second) : imaginons qu’après un meurtre on détecte sur l’arme du crime les empreintes digitales du meurtrier présumé, on pourra conclure, avec un risque d’erreur, à sa culpabilité ; mais si on ne trouve pas d’empreintes, on ne conclura pas pour autant que le sujet est innocent, on dira seulement qu’on n’a pas prouvé sa culpabilité (non conclusion).
 

La dissymétrie des mots

Le premier risque, déclarer active une drogue qui ne l’est pas, est considéré par tous comme une erreur. Quel scientifique ne serait pas désolé de publier une telle contrevérité ? Le second risque par contre ne mérite pas vraiment cette qualification : laisser échapper une drogue active, un médicament efficace contre le cancer par exemple, est certes regrettable, davantage peut-être que le premier risque, mais cette non conclusion n’est pas une erreur, c’est un « manque à gagner ». Aussi beaucoup de statisticiens, dont je suis, réservent-ils le mot erreur au premier risque. Quel meilleur argument pourrait-on alors avancer à cet égard que la comparaison avec le domaine de la justice ? Condamner un innocent est une erreur judiciaire, laisser échapper un coupable ne l’est pas - quel que puisse être le danger de cette décision.
 

Combien d’erreurs ?

Un statisticien décide, pour l’écart significatif, d’adopter le risque de 5%. Cela veut-il dire qu’il se trompera, en moyenne, 5 fois sur 100 ? Non. Voici en effet, en reprenant l’exemple des souris à cancer, le nombre d’erreurs attendu, sur une longue série de drogues présentées, en comportant n inactives et n’ actives :

• pour les n drogues inactives : n x 5%
  
  
• pour les n’ drogues actives : 0 (en effet, ou le statisticien conclura « actif » et il aura raison, ou il ne conclura pas, nous avons convenu que c’était un « manque à gagner » mais pas une erreur).

Le nombre d’erreurs sera donc au total n x 5% sur les (n + n’) drogues soit un pourcentage d’erreurs valant (n x 5%)/ (n+n’) ou [n/(n+n’)] x 5%

Si le statisticien travaille avec un biologiste qui a du flair, et ne lui apporte que des drogues actives (n = 0), le pourcentage d’erreurs sera nul. Si le biologiste est un piteux chercheur, et n’apporte jamais de produits actifs (n’ = 0) ce pourcentage sera de 5%. La réalité sera bien sûr entre ces deux extrêmes, mais il s’agit le plus souvent de soumettre à expérience des drogues plausiblement actives, le rapport n/(n + n’) sera faible, le pourcentage d’erreurs nettement inférieur à 5%. Transposé de cet examen de drogues à un ensemble de phénomènes soumis à vérification statistique, phénomènes traduisant le plus souvent des hypothèses plausibles, le pourcentage d’erreurs est nettement inférieur à 5%. Ce qui est fort heureux, car admettre 5% d’erreurs, vu l’énorme quantité de recherches effectuées, conduirait à un nombre de publications erronées tout à fait inacceptable.

On peut, ici encore, évoquer l’analogie avec le jugement d’un tribunal : si a est le risque, pour un innocent, d’être condamné (a est la notation consacrée en statistique, c’est le 5% envisagé ci-dessus, je ne me hasarderai pas à lui fixer ici une valeur…), il y aura, sur une série de jugements :

n innocents donnant lieu à : n x α erreurs judiciaires, et n’ coupables ne donnant lieu à aucune erreur judiciaire. Soit en tout n x α erreur judiciaires, ou en pourcentage [n / (n + n’)] x α.

Le pourcentage d’erreurs judiciaires sur une série de jugements sera donc inférieur ou au plus égal à a, d’autant plus inférieur qu’une instruction plus soignée du dossier aura conduit au tribunal moins d’innocents et davantage de coupables (sans doute est-ce évident, mais c’est en cela que l’analogie éclaire le problème général, pour lequel cette évidence échappe souvent).
 

L’antagonisme des deux risques

On a vu clairement qu’à vouloir diminuer le premier risque, on augmentait le second. Cet antagonisme des deux risques est une réalité bien banale : si dans un examen on décide d’être plus sévère, on recevra moins de mauvais élèves, mais on en recalera plus de bons. Cependant c’est dans le domaine de la justice que le problème a fait l’objet d’innombrables débats passionnés entre mathématiciens, philosophes et politiques. Condorcet le premier proposait en 1’785 une formule permettant, sous certaines hypothèses, de calculer la probabilité de condamner un innocent. Laplace en 1830, précisant la formule, l’appliquait aux jugements en Cour d’Assises, où les jurys comprenaient douze juges, la condamnation étant prononcée à la majorité (7 voix contre 5). Laplace montrait que le risque d’erreur était alors de 1/4, valeur manifestement intolérable ! A l’arrivée des libéraux aux affaires, en 1830, la proportion était reportée à 8 voix contre 4 ; mais même avec cette modification, le risque d’erreur restait encore très élevé, Arago exposait à la Chambre des Députés que « sur 8 hommes qui montent à l’échafaud, il y en a un d’innocent » ! Et de proposer de rabaisser le risque à 1/16… Si les multiples débats et les centaines d’ouvrages consacrés à la « statistique des jugements » ne sont pas l’ébauche du test statistique, elles partent de ses prémisses : « il est de notre nature, remarquait Condorcet, de ne pouvoir juger que sur des probabilités, il n’est donc pas injuste de condamner un innocent, pourvu que l’on soit assuré qu’il y a une grande probabilité que la décision rendue soit exacte ». C’était bien proposer la politique du risque consenti, avec intervention du calcul des probabilités. Et si l’on considérait comme obligatoire d’envoyer un innocent à l’échafaud, le plus rarement possible, mais quand même de temps à autre, c’est bien qu’on prenait en compte, implicitement sinon explicitement, l’autre risque, celui de relaxer un coupable…

Daniel Schwartz
 

1. Sans doute est-il plus intéressant de diminuer que d’augmenter la fréquence des cancers… mais la formulation proposée est plus simple : elle peut d’ailleurs n’être pas sans intérêt sur le plan scientifique.

 
Pénombre, Décembre 1995