L’évaluation des CP dédoublés
De nombreux médias se sont fait le relais du communiqué de presse de Jean-Michel Blanquer concernant les premiers résultats de l’expérimentation des CP dédoublés. Ainsi, le journal Le Monde publié le 23 janvier 2019 y consacre un article Première évaluation en demi-teinte pour les CP dédoublés. Je lis : « L’étude d’impact de cette mesure porte sur un échantillon de 15 000 élèves de REP+, comparés à un groupe test d’élèves de REP qui n’ont pas bénéficié du dédoublement mais présentent un profil sociologique similaire. »
Mais les conclusions me surprennent : « Sur les 60 000 élèves de CP en REP+, la proportion de ceux qui sont les plus en difficulté a baissé de 7,8 % en français et de 12,5 % en mathématiques. » Avant d’accuser les journalistes de généralisation hâtive, visitons le site de la Direction de l’évaluation, de la prospective et de la performance (DEPP) du ministère de l’Éducation nationale qui a été chargée de l’étude. Les journalistes n’ont rien inventé, c’est du copier-coller du dossier de presse publié sur le site et il ne semble pas qu’un rapport plus approfondi soit présent.
Selon ce dossier de presse, quels sont les résultats en français et en maths ? On aimerait avoir des résultats bruts, des moyennes, des médianes, des écart-types, mais point du tout. On en sait seulement que « l’évaluation de l’impact du dédoublement sur les compétences des élèves indique que l’effet est de 8 % d’écart-type en français et de 13 % en mathématiques, en faveur des élèves de REP+, par rapport au groupe témoin » et que « cet effet est donc statistiquement très significatif ». 8 % d’écart-type, cela ne parle pas beaucoup et il serait facile d’en conclure que l’effet est de 8 % de baisse du nombre des élèves en difficulté. Heureusement une note de bas de page indique : « L’effet d’une politique de réduction de la taille des classes est mesuré en pourcentage d’écart-type de score, c’est-à-dire en termes de différence de score moyen entre le groupe témoin et le groupe de référence, rapportée à l’unité du score (son écart-type). Ceci permet de rendre comparable les différentes mesures de performances ».
Concrètement, ça veut dire quoi ? Cet indice est souvent proposé dans ce type d’étude, souvent aussi assorti d’autres indices statistiques. Il faut déjà comprendre que les pourcentages annoncés (8 % d’écart-type en français et de 13 % en mathématiques) ne se réfèrent pas à un pourcentage d’élèves.
Donc, ces résultats restent quelque peu abstraits et on peut se demander quelle différence de performances ils peuvent refléter, au moins approchée. Comment peut-on concrètement se représenter cet écart entre les deux groupes ?
Le calcul de ce coefficient se fait, comme indiqué dans l’article de la DEPP, selon la formule :
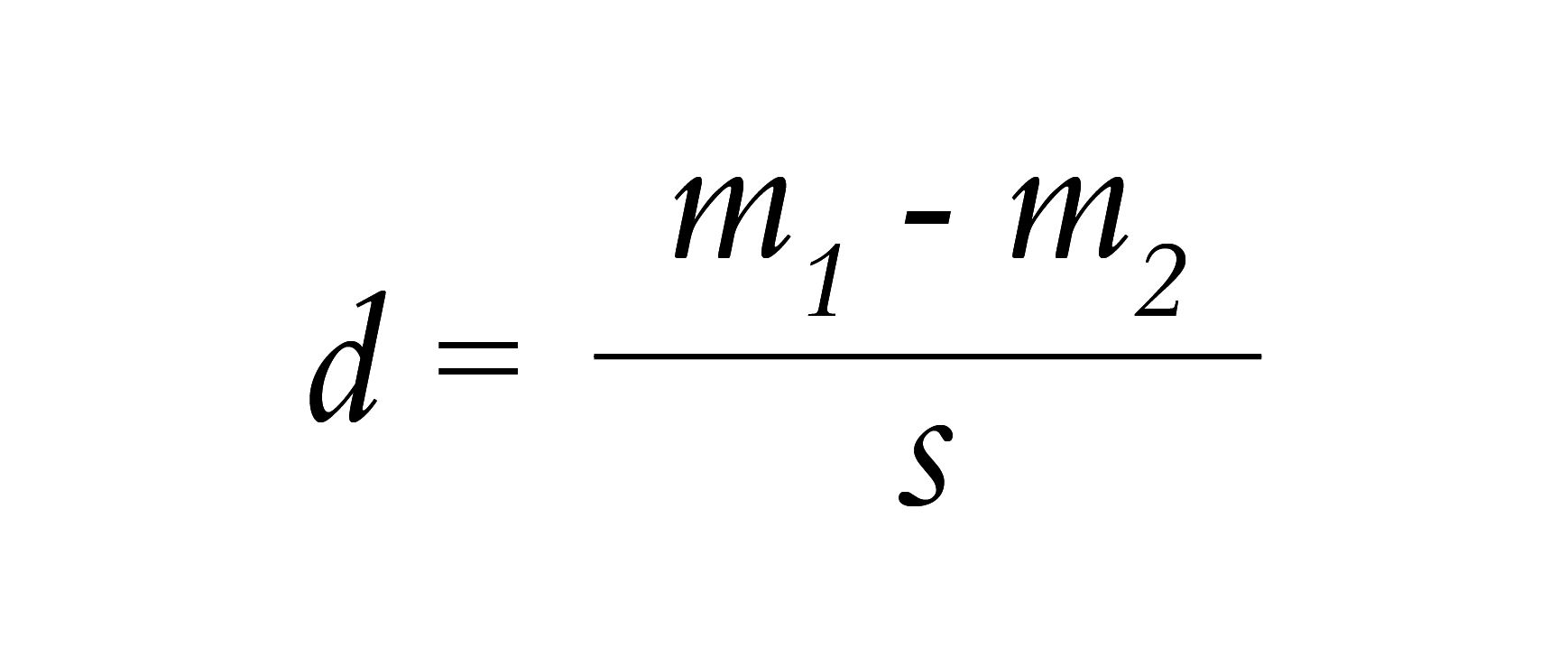
où m1 et m2 sont les moyennes des notes obtenues dans les 2 groupes à comparer et s est l’écart-type combiné de ces notes. Prenons pour exemple fictif des notes sur 20 (restons classique) avec un écart-type combiné de 3 (vraisemblable si la distribution est normale) et appliquons ces valeurs à la différence de 8 % d’écart-type en français :
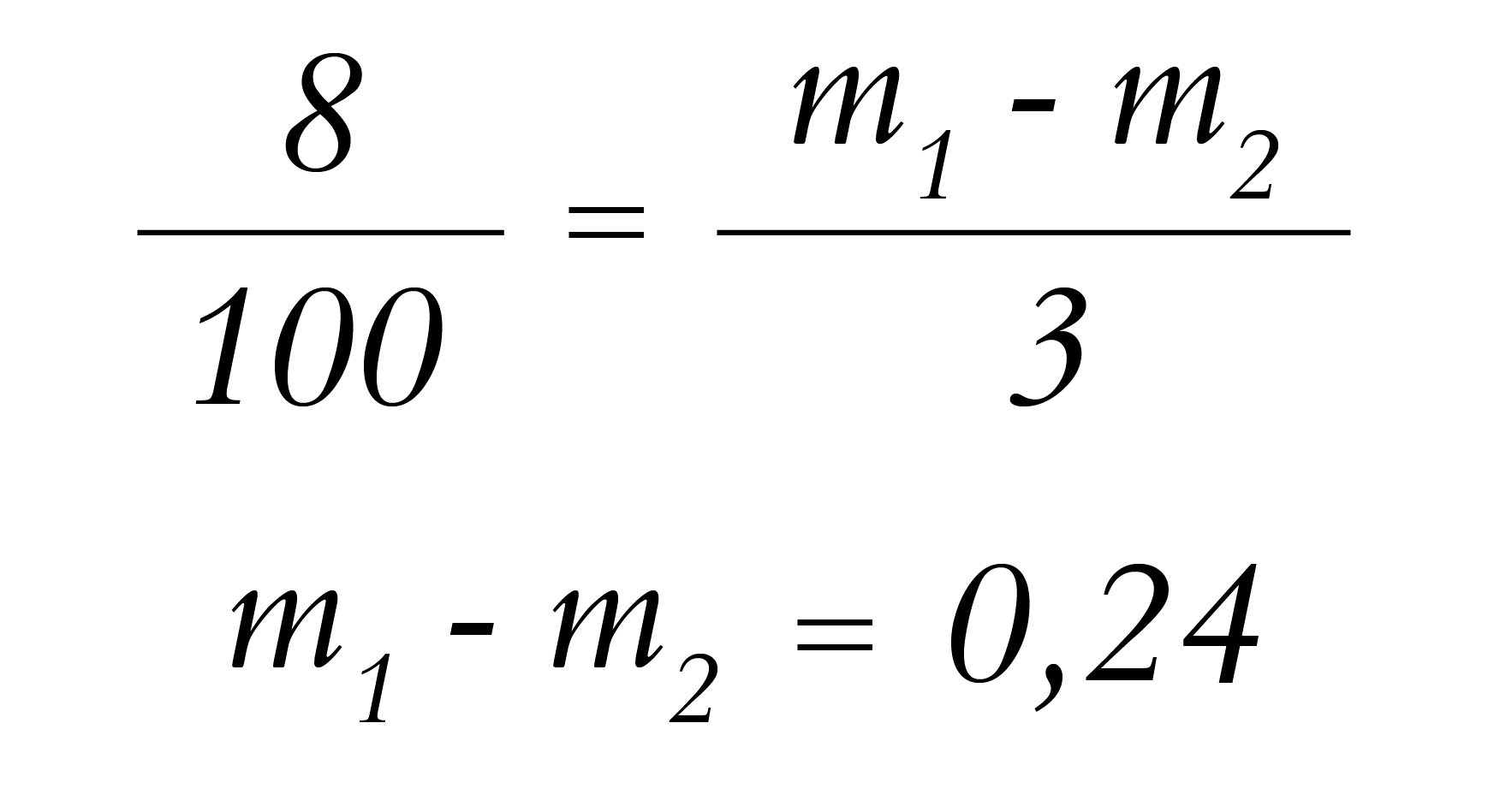
Donc, avec des notes sur 20, il y a 0.24 points de différence entre les moyennes des 2 groupes, soit même pas un quart de point.
Une autre manière de se représenter cet écart est de considérer un élève qui aurait 7 sur 20 sans dédoublement. Il devrait gagner 3 points, c’est-à-dire un écart-type, pour obtenir la moyenne de 10. Le dédoublement lui fait seulement gagner 0.08 points.
Un autre calcul est souvent présenté dans ce type d’étude permet de réaliser qu’un élève qui serait 12ème sur 24 dans une classe normale n’aurait plus que 11,23 élèves devant lui en français (il aurait gagné moins d’une place…) et 10,76 élèves devant lui en maths, il aurait gagné une place (voir l’encadré ci-après).
C’est également ce qu’il ressort de l’avis des chercheurs présentés par la note de la DEPP comme « chercheurs reconnus » lui ayant apporté leur concours. Le Monde écrit : « Au regard de la littérature scientifique sur le sujet, les résultats se situent plutôt dans la “fourchette basse” de ce que l’on pouvait attendre, puisque les dispositifs de cette nature produisent en moyenne un gain de 8 à 12 places dans un classement d’élèves. “ Les politiques éducatives ne produisent parfois aucun effet, une hausse de cette ampleur est donc déjà significative ”, précise Julien Grenet, chercheur à l’Ecole d’économie de Paris qui a contribué à construire l’évaluation. »
Lequel Julien Grenet a confirmé cette opinion qui est la sienne lors d’une émission de France Culture le 3 mars 20109 en disant que, par rapport aux autres études en France dans d’autres pays, les 8 % et 13 % d’écart-type se situent dans la fourchette basse. Il a également qualifié l’écart de significatif mais plus faible qu’ailleurs.
L’article du Monde poursuit ainsi : « Un constat partagé par Marc Gurgand, coauteur avec Julien Grenet, d’une note de l’Institut des politiques publiques (IPP), parue en septembre 2017 sur le sujet. Les résultats “ sont clairement dans le bas de la fourchette de ceux constatés dans d’autres pays qui ont mis en œuvre de telles mesures, mais ils sont déjà significatifs ”, a déclaré le chercheur, interrogé par l’AFP. “ Il est rare qu’on trouve des effets de cet ordre de grandeur pour des politiques scolaires menées à si grande échelle. ” »
Les progrès réalisés par cet échantillon d’élèves sont donc bien dans le bas de la fourche.
Généralisation des résultats. « Cet effet est donc statistiquement significatif » indique le texte de la DEPP, même si aucune donnée présentée dans ce texte ne permet de le savoir. Au mieux, cela signifierait qu’on peut penser qu’une différence non nulle serait obtenue dans la population dont cet échantillon est extrait.
« Cet effet se vérifie en particulier pour les élèves en très grande difficulté : sur les 60 000 élèves scolarisés en CP REP+ l’année dernière, 40 % étaient en très grande difficulté en mathématiques et en français soit 24 000 élèves ; le dispositif permet une baisse de cette proportion d’élèves en très grande difficulté de 7,8 % pour le français et de 12,5 % en mathématiques ; ainsi, au terme de la première année, sur les 24 000 élèves en très grande difficulté, il y a (c’est nous qui soulignons) :
- 2 000 élèves de moins en très grande difficulté en français ;
- 3 000 élèves de moins en très grande difficulté en mathématiques. »
De manière très rustique, la DEPP se contente donc d’appliquer un coefficient multiplicateur pour passer des 15 000 élèves de l’échantillon aux 60 000 élèves de REP+, et rustiquement aussi, elle arrondit les « 2 000 » et « 3 000 »... À la louche ?
Quarante pourcent d’élèves en très grande difficulté, diable ! Comment les repère-t-on ? et combien sont seulement en moyenne difficulté, en petite difficulté ? Mais bon, soustraire 7.8 % ou 12.5 % d’élèves à ce groupe, c’est déjà bien.
En guise de conclusion (temporaire). Ce n’est pas parce que le bébé n’est pas aussi beau que prévu qu’il faut….Toutes les imperfections que nous venons de signaler ne sauraient à elles seules amener à conclure à la faible efficacité du dédoublement. En effet, ces imperfections permettent de laisser entrevoir d’autres résultats dans d’autres conditions d’expérimentation. On sait que les conditions-mêmes d’une évaluation jouent sur les performances mesurées. Le choix des exercices, leur longueur, leur présentation, le mode de réponse etc. c’est l’ensemble de ce dispositif qui est évalué et non seulement le dédoublement. Le document de la DEPP insiste à plusieurs reprises sur le fait que « l’enquête souligne que, pour être pleinement efficace, le dédoublement des classes doit s’accompagner d’une transformation en profondeur des pratiques pédagogiques ». De quelle transformation s’agit-il ? Comment les tester indépendamment des autres variables ? Autant de questions devraient permettre de ne pas se contenter d’une réflexion coût /efficacité en se fondant sur une telle évaluation.
Kéréva
Gagner de la place...
On suppose que la distribution des notes est normale, et ramenée à la loi normale centrée réduite N(0 ;1). J’appelle Z une variable suivant cette loi.
Gagner un écart-type, c’est se déplacer d’un écart-type vers les bonnes notes, de +1, donc. L’élève médian passe de Z = 0 à Z = 1. Or p(0 < Z < 1) ≈ 0,34.
Cela peut être vu comme un gain de 34% de places (soit 34 places dans un groupe de 100, ou 8,16 places dans un groupe de 24).
Gagner 8 % d’écart-type, c’est se déplacer de +0,08 . L’élève médian passe de Z = 0 à Z = 0,08. Or p(0 < Z < 0,08) ≈ 0,032.
Cela peut être vu comme un gain de 3,2 % de places (soit 3,2 places dans un groupe de 100, ou 0,77 place dans un groupe de 24).
Mais tout ça, c’est juste une façon de donner un peu de chair à cette histoire de gain en écart-type. Il n’y a aucune raison que la distribution des notes soit normale. Et le gain de place calculé, qui ne concerne que l’élève médian, n’est qu’une image.